↓跳过正文
  1. Posts/
  2. algorithm/

以 skrl 库为例的 PPO 算法调参指南

·450 字·3 分钟
Haoran Zhou | 周浩然
作者
Haoran Zhou | 周浩然
海阔凭鱼跃
目录

下面使用到的参数以 skrl 库为例，不同 RL 算法库之间的参数命名可能不一样。

rewards_shaper_scale
#

在 skrl 中，可以通过设置缩放系数 rewards_shaper_scale 来对奖励进行缩放。

推荐修改 skrl 中的 runner.py 的 reward_shaper_function，将缩放函数调整为动态计算奖励的 running mean 和 running var 对奖励归一化处理，其代码为

class RewardScaling:
    def __init__(self, shape, gamma):
        self.shape = shape  # reward shape=1
        self.gamma = gamma  # discount factor
        self.running_ms = RunningMeanStd(shape=self.shape)
        self.R = np.zeros(self.shape)

    def __call__(self, x):
        self.R = self.gamma * self.R + x
        self.running_ms.update(self.R)
        x = x / (self.running_ms.std + 1e-8)  # Only divided std
        return x

    def reset(self):  # When an episode is done,we should reset 'self.R'
        self.R = np.zeros(self.shape)

kl_threshold
#

KL 散度描述了当前更新的策略和上一个策略相比的变化情况，由于 PPO 在一次迭代中使用同一批数据进行策略更新，因此不能让策略变化过大，需要对 KL 散度进行限制，通过设置一个最大kl值kl_threshold，在每次迭代中当达到这个最大kl就停止这次迭代。 对应 skrl 中的代码:

# early stopping with KL divergence
if self._kl_threshold[uid] and kl_divergence > self._kl_threshold[uid]:
    break

在 skrl 中，kl_threshold 默认设置为 0，即不使用早停。在 rl_games 中，这一参数默认设置为 0.008

举个例子：

情景A: 训练时如果发现 policy loss 呈震荡趋势（如下图），并且策略不收敛，可能是多种原因导致的，首先可以排查 KL 散度的问题。

alt text
观察训练时的 KL 散度，发现 KL 散度值在 0.7 左右波动，说明策略的变化过大，可以将阈值设置为 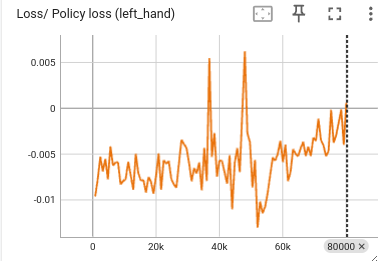kl_threshold=0.01。
alt text
重新训练后，策略更新变得平稳许多。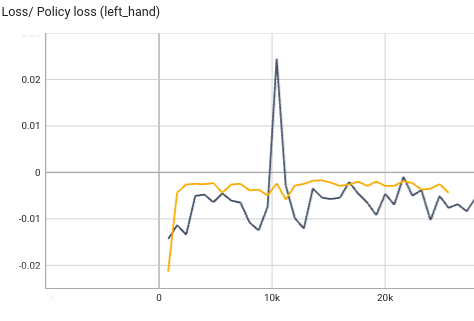

情景B: 训练时如果发现 reward 突然下降（如下图），那么一定是策略的探索行为导致了破坏性的更新。

alt text
观察训练时的 KL 散度（如下图），发现 KL 散度值在 1e-4~1e-3 区间内波动，而在某一时刻，KL 达到了 0.002，而这一时刻正对应着 reward 开始下降的时刻。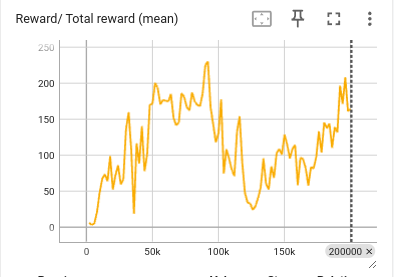
alt text
这说明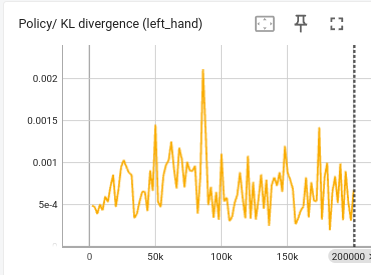，kl_threshold=0.01对于当前训练的任务来说还是太高了，策略发生稍微较大的更新就会破坏学习，可以尝试重新调整为kl_threshold=0.001。

针对情景B，reward 突然下降这一问题，在知乎回答中【whycadi​】也提到，办法之一是“要限制最终采样的动作值的范围，减小学习率。”。这其实和早停方法的道理是一样的，我们通过早停方法来限制策略的更新，避免过度向外采样。

Learning rate scheduler - KL Adaptive
#

skrl 默认使用 KLAdaptiveLR 作为学习率调度器，该调度器也接受一个名为 kl_threshold 的参数，其更新策略为:

IF KL > kl_threshold * kl_factor THEN
next_lr = max(lr / lr_factor, min_lr)
IF KL < kl_threshold / kl_factor THEN
next_lr = min(lr * lr_factor, max_lr)

默认值： kl_threshold: float = 0.008, min_lr: float = 1e-6, max_lr: float = 1e-2, kl_factor: float = 2, lr_factor: float = 1.5,

举个例子，假如设置 kl_threshold=0.008，其它参数使用默认值。 如果 KL 散度值超过阈值 0.008*2=0.016 ，学习率会开始下降，避免策略更新过猛。当小于阈值 0.008/2=0.004 时，说明策略更新幅度小，调度器会增加学习率。

learning_rate_scheduler_kwargs:
    kl_threshold: 0.008

针对情景B，也可以尝试降低该调度器中的 kl_threshold。 然而，如果kl_threshold设置的过低，会限制策略的探索能力，容易收敛到局部最优解。

discount factor - gamma
#

这一参数【曾伊言】已经讲解的非常清楚，因此直接将原文复制过来：

这个值的含义是“你希望你的智能体每做出一步，至少需要考虑接下来多少步的reward？”如果我希望考虑接下来的t 步，那么我让第t步的reward占现在这一步的Q值的 0.1， 即公式 $0.1\approx\gamma^t$ ，变换后得到：$\gamma\approx 0.1^{1/t}$

gamma ** t = 0.1  # 0.1 对于当前这一步来说，t步后的reward的权重
gamma = 0.1 ** (1/t)
t = np.log(0.1) / np.log(gamma)

0.9   ~= 0.1 ** (1/  22)
0.96  ~= 0.1 ** (1/  56)
0.98  ~= 0.1 ** (1/ 114)
0.99  ~= 0.1 ** (1/ 229) 
0.995 ~= 0.1 ** (1/ 459)
0.999 ~= 0.1 ** (1/2301)  # 没必要，DRL目前无法预测这么长的MDPs过程

可以看到  0.96, 0.98, 0.99, 0.995 的gamma值
分别对应    56,  114,  229,   459 的步数

调整 gamma 的意义在于加速收敛。如果 gamma 过于大，意味着越多考虑未来的奖励，而未来的不确定性更多，超出了智能体所能掌控的范围。 gamma绝对不能选择1.0，gamma等于或过于接近1会有“Q值过大”的风险。一般选择0.99，在某些任务上需要调整。 而如果 gamma 选的很小，智能体只会关注短期回报，可能导致陷入局部最优。

rollouts，num_envs
#

rollouts 对应 rl_games 中的 horizon_length

rollouts： 与环境交互的次数，rollout 一次，可以得到 num_envs 条 transitions，每次 update 前，可以收集到 rollouts * num_envs 条 transitions。

假设 rollouts=96, num_envs=128，那么每次 update 时的 buffer size 为 12288（~2^13.5）。因

此，并行环境数量 num_envs 实际上也是一个我们需要去调整的超参数，该参数通常根据计算机性能来选择。先确定 num_envs，再确定 rollouts。

为了尽可能准确地用多条轨迹去描述环境与策略的关系，在随机因素大的环境中，推荐增加 rollouts 的值以加大采样步数。

mini_batches
#

mini_batches = rollouts * num_envs / batch_size，

这里的 batch_size 对应 rl_games 中的 minibatch_size

同理，

batch_size = rollouts * num_envs / mini_batches，

假设 batch_size = 2**12(4096)，num_envs=128， rollouts=96，可以计算出 mini_batches=3

假设 batch_size = 2**12(4096)，num_envs=128， rollouts=128，可以计算出 mini_batches=4

对于 on-policy 算法，batch_size 推荐选取范围为（2**9 ~ 2**14），batch_size 越大，训练越慢，但更容易获得单调上升的学习曲线。

learning_epoch
#

对应 rl_games 中的 mini_epochs

对应【曾伊言】提到的数据复用次数 reuse_times（不是 update_times）。该参数一般设为 8，可以从偏小的数值开始尝试，以避免过拟合。

time_limit_bootstrap
#

该参数使用在 skrl 中的 on-policy 算法上，默认为 False。

在强化学习中，环境的 episode 可能因为时间限制而提前结束，而不是因为任务自然完成（如达到终止状态）。 如果将时间限制终止（truncation）视为失败并将最终奖励设为 0，会导致值函数低估这些状态的真实价值。 为了修正这个问题，time_limit_bootstrap 允许在 episode 因时间限制而终止时，用值函数的预测值来补偿最终奖励，从而减少不必要的值函数低估。 因此，建议将该值设置为 True

# time-limit (truncation) bootstrapping
if self._time_limit_bootstrap[uid]:
    rewards[uid] += self._discount_factor[uid] * values * truncated[uid]

参考博文
#